
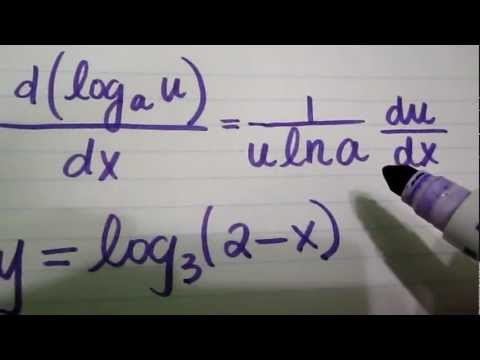
So once again, you take the derivative with respect to x of the natural The nth derivative of log left 3x + 4 right is dfrac3n 1n 1n 13x + 4n ReasonR IF y log left ax + b right then yn dfrac 1n 1n 1anax + bn A Both A and R are. And it does indeed, let me do this in a slightly different color, it does indeed look like functions for the trigonometric functions and the square root, logarithm and exponential function.
#Derivative of log 3x free
from domain of composite Derivatives of logarithmic functions are mainly based on. Solve derivatives using this free online calculator. Calculator supports derivatives up to 10th order as well as complex functions. It allows to draw graphs of the function and its derivatives. Right over here, when x is equal to 1/2, one over 1/2, the slope should be two. fog gof calculator 3 x (number of inches over 5ft tall) for females. Derivative Calculator computes derivatives of a function with respect to given variable using analytical differentiation and displays a step-by-step solution.
#Derivative of log 3x plus
The derivative of ln (3x) is expressed as f (x) equals ln (3x) The expression ln (3x) can be separated as ln (x) plus ln (3). Natural log of four, but the slope of the tangent line here looks pretty close to 1/4 and if you accept this, it is exactly 1/4, and you could even go The symbol ln is used for a natural log function. When x is equal to four, this point is four comma What's the slope here? Well, it looks like, let's see, if I try toĭraw a tangent line, the slop of the tangent line Here is the natural log of two, but more interestingly, What about when x is equal to two? Well, this point right over Over one is still one, and that seems like what This is the derivative of 100, minus 3 times, the derivative of. I can use the sum rule and constant multiple rule. This is the derivative of 100 minus 3 log x. Remember, when you see log, and the base isn't written, it's assumed to be the common log, so base 10 log. Tangent line look like? Well, it looks like here, the slope looks like it is equal, pretty close to being equal to one, which is consistent with the statement. Let's find the derivative of 100 minus 3 log x. Our next task is to determine what is the derivative of the natural logarithm.

If you have a function f(x), there are several ways to mark the derivative of f when it comes to x.The common way that this is done is by df / dx and f(x).If a derivative is taken n times, then the notation d n f / d x n or f n (x) is used. So let's say right over here, when x is equal to one, what does the slope of the What is Derivatives In math, a derivative is a way to show the rate of change or the amount that a function is changing at any given point. To apply the Chain Rule, set u u as 3 x 3 x. And just to feel good about the statement, let's try to approximate what the slope of the tangent y log(3x) y log ( 3 x) Differentiate using the chain rule, which states that d dx f (g(x)) d d x f ( g ( x)) is f '(g(x))g'(x) f ( g ( x)) g ( x) where f (x) log(x) f ( x) log ( x) and g(x) 3x g ( x) 3 x. Differentiate using the chain rule, which states that ddxf(g(x)) d d x f ( g ( x ). So right here is the graph of y is equal to the natural log of x. Just going to appreciate that this seems like it is actually true. In a future video, I'mĪctually going to prove this. With respect to x of the natural log of x's. That derivative approaches 0, that is, becomes smaller.ī) when x is less than 1 and becomes smaller.Video, we're going to think about what the derivative Calculate the derivative of lnĪccording to the rule for changing from base e to a different base a:Ī) when x is greater than 1 and becomes larger. When y = e u( x), then according to the chain rule:Įxample 4.

The derivative of e with a functional exponent In the system of natural logarithms, in which e is the base, we have the simplest constant possible, namely 1. ( Lesson 39 of Algebra.) When we calculate that derivative below, we will see that that constant becomes ln a. Where k is the constant of proportionality. Therefore, to say that the rate of growth is proportional to its size, is to say that the derivative of a x is proportional to a x. The more individuals there are, the more births there will be, and hence the greater the rate of change of the population - the number of births in each year.Īll exponential functions have the form a x, where a is the base. The bigger it is at any given time, the faster it's growing at that time. For we say that a quantity grows "exponentially" when it grows at a rate that is proportional to its size.

What does that imply? It implies the meaning of exponential growth.


 0 kommentar(er)
0 kommentar(er)
